BOJ 2309. 일곱 난쟁이

BOJ 2309. 일곱 난쟁이

풀이

9 난쟁이 중 7 난쟁이가 아닌 2 난쟁이를 찾는 문제이니 나올 수 있는 경우의 수를 계산해보면
순서를 고려하지않고 n중 r을 찾는 경우이므로, 조합 nCr에 대입하면

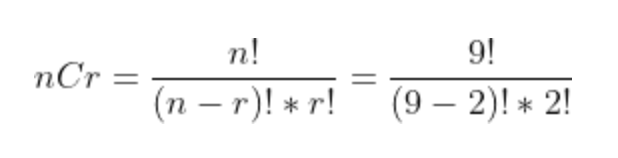
이므로 36이다.

경우의 수가 적으니 모든 경우의 수에 대입하여 정답을 찾아보도록 한다.
7 난쟁이의 키의 합이 100이니
7 난쟁이가 아닌 2명을 제외하였을 때 키가 100이면 정답이다.

import java.io.IOException;
import java.util.Arrays;
import java.util.Scanner;

class Main {
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int[] a = new int[9];
        int sum = 0;

        for (int i = 0; i < 9; i++) {
            a[i] = sc.nextInt();
            sum += a[i];
        }

        Arrays.sort(a);

        for (int i = 0; i < 9; i++) {
            for (int j = i + 1; j < 9; j++) {
                if ((sum - a[i] - a[j]) == 100) {
                    for (int k = 0; k < 9; k++) {
                        if (k != i && k != j) {
                            System.out.println(a[k]);
                        }
                    }
                    sc.close();
                    System.exit(0);
                }
            }
        }
    }
} 

import kotlin.system.exitProcess

fun main() {
    val a = (0 until 9).map { readLine()!!.toInt() }.toList().sorted()
    val sum = a.sum()

    for (i in 0 until 9) {
        for (j in i + 1 until 9) {
            if ((sum - a[i] - a[j]) == 100) {
                (0 until 9)
                    .filter { it != i && it != j }
                    .map { a[it] }
                    .forEach(::println)
                exitProcess(0);
            }
        }
    }
} 

풀이소스

github.com/beomjo/algorithm-study/commit/50e5df0644164843f65b928f04d2b46d1468e9c7